DFCI Logo
DFCI Logo

Program in Regulatory Science Clinical Trial Designs

    In this section

    The work of the Program in Regulatory Science focuses on the development, application, theoretical study, and software for innovative clinical trial designs. Areas of our research include:

    Platform Designs

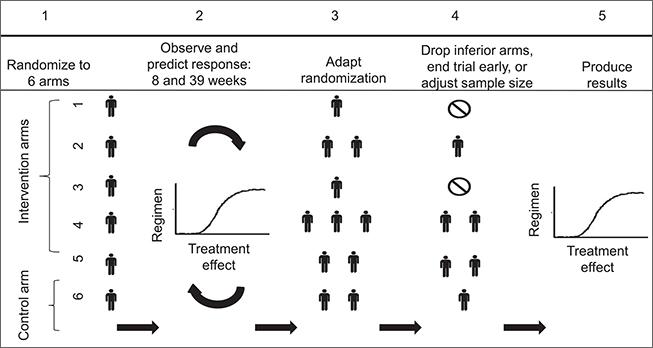
    We study platform designs, which allow investigators to add new and remove existing experimental arms on a clinical study, either when new experimental drugs become available, or when sufficient information on the efficacy of an experimental treatment has been gathered. Although controlled multi-arm trials are more efficient than two-arm studies, because the control arm is not replicated to evaluate multiple treatments, they are rarely utilized. A drawback is the requirement that all therapies, often drugs from different companies, must be available for testing at the onset of the trial. Platform trials, by contrast, remedy this constraint and can substantially improve the efficiency of screening studies that evaluate new treatments in their early stages of development.

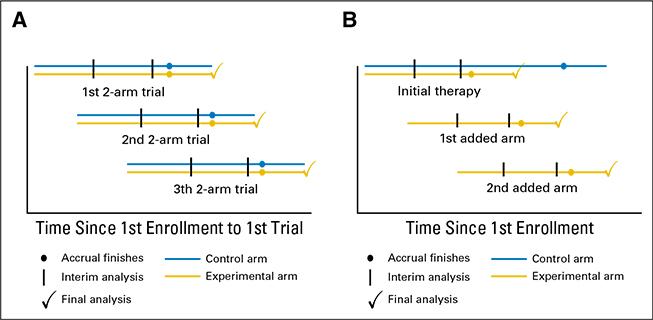
    (A and B) Comparison of the (B) rolling-arms design and (A) independent two-arm trials. The rolling-arms design starts with one experimental arm, and two arms are added later during the trial. Blue and gold lines indicate control and experimental arms, and vertical lines indicate interim analyses. For each experimental arm k, the beginning and end of the corresponding gold line indicate the time of onset of the active accrual period of arm k and the final analysis for arm k.

    Read more: Ventz et al 2017, Designing Clinical Trials That Accept New Arms: An Example in Metastatic Breast Cancer, Journal of Clinical Oncology

    Definition of Adaptive Randomization Probabilities

    We propose new Bayesian response-adaptive randomization rules. Most response-adaptive randomization schemes have been designed to increase the number of patients that receive an effective treatment during the clinical trial. We developed approaches to translate early evidence and available information on treatments into suitable randomization probabilities during the course of the study. In multi-arm studies, we define Bayesian randomization probabilities that, at completion of the study, minimize uncertainty of the treatment effects of multiple experimental arms as quantified by standard statistical metrics.

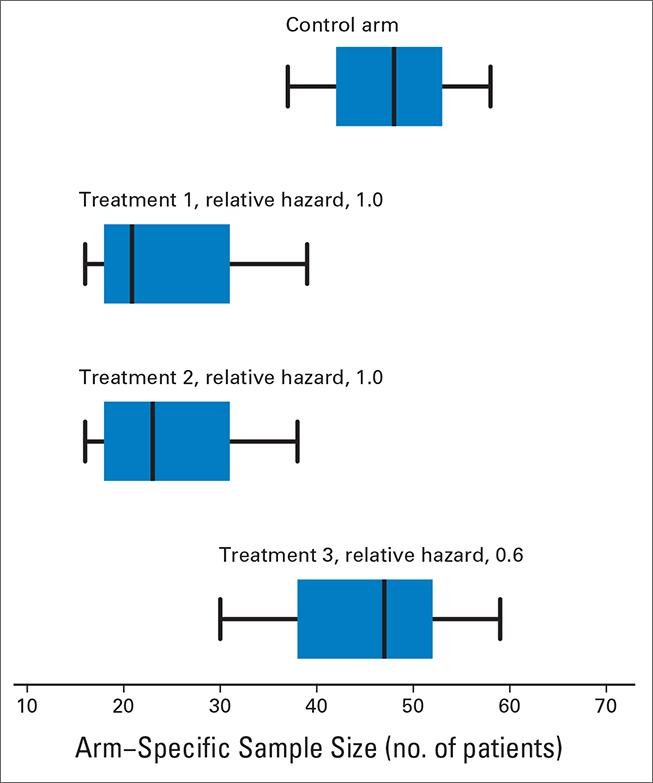
    Read more: Trippa et al 2012, Bayesian adaptive randomized trial design for patients with recurrent glioblastoma, Journal of Clinical Oncology

    Biomarker-Driven Clinical Trials

    Biomarkers define patient subgroups, which are fundamental in clinical studies where investigators expect different treatment effects across biomarker profiles; the primary goal is to identify the subpopulation for which the experimental therapy shows evidence of treatment efficacy and to exclude other subpopulations for which it does not. To facilitate this, Bayesian response-adaptive designs map accumulating information on experimental treatments into randomization probabilities that vary across patient subgroups. We recently studied the use of Bayesian adaptive randomization in basket clinical trials, which enroll multiple cancer types. We modeled the treatment effects by allowing variations both across cancer types and across biomarker subgroups.

    Incorporation of biomarker data into clinical trials. The traditional basket (TB) and biomarker agnostic (BA) trials are nonadaptive and either enroll only biomarker-positive patients (TB) or all patients (BA) throughout the course of the trial. Although TB may provide efficiency if the original hypothesis of a biomarker-treatment effect linkage is correct, nothing new is learned about the biomarker. Adaptive multistage trials can start with either biomarker-only patients or all patients and then decide how to proceed further after an interim analysis. The Bayesian basket design sets the initial randomization probabilities of patient subgroups to multiple experimental arms and a control by incorporating explicit a priori judgments based on preclinical and other clinical experience. The trial then functions to maximize learning about both the experimental agent treatment effects and their variation in the biomarker-positive and -negative subgroups during the course of the trial, and it adjusts the randomization probabilities accordingly. In this Bayesian Basket example, there are three different arms on the same trial depicted. The leftmost arm starts out as a TB trial based on the investigators’ weighing of prior data and stays that way throughout the trial. The middle arm starts out rather uncertain about the biomarker-effect linkage but then learns that the signal is limited to the biomarker-positive population only. Finally, the rightmost arm starts with preliminary evidence that the biomarker-positive group would uniquely benefit from the therapy, but during the course of the trial, it becomes evident that all patients might benefit.

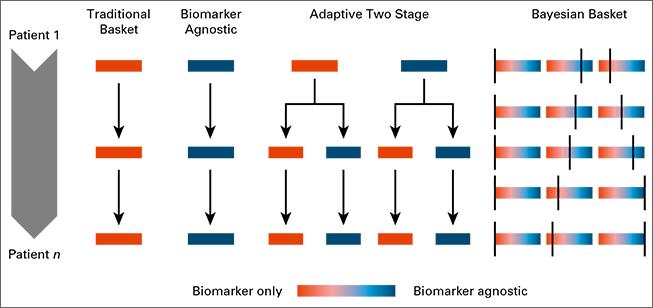
    Read more: Trippa Alexander 2016, Bayesian Baskets: A Novel Design for Biomarker-Based Clinical Trials, Journal of Clinical Oncology

    Joint Modeling of Multiple Endpoints

    Our collaborations motivated work on joint Bayesian modeling of surrogate and primary endpoints. The goal of this work is to produce randomization probabilities that mirror, during the course of the clinical trial, both early efficacy results for surrogate endpoints and preliminary evidence of treatment effects for primary endpoints. In cancer trials, we use the duration of progression-free status to predict patient survival using Bayesian methods. Joint modeling of multiple endpoints allows us to use adaptive randomization in clinical settings where the primary outcome becomes available months or years after treatment assignment.

    Read more: Trippa et al 2015, Combining progression-free survival and overall survival as a novel composite endpoint for glioblastoma trials, Neuro Oncology

    False Positive Results, P-values and Bayesian Studies

    We propose and study methods that allow frequentist analyses, including rigorous p-values and confidence intervals, at completion of Bayesian clinical trials. Clinicians, scientific review panels, and other stakeholders in the clinical trials arena are familiar with key statistical concepts from the frequentist literature: type I error rates, hypothesis testing and confidence intervals to name a few. Methodologies that combine Bayesian designs and frequentist analyses can accelerate the adoption of innovative adaptive designs, and simplify their acceptance from stakeholders involved in clinical studies.

    Read more: Ventz et al 2015, Bayesian designs and the control of frequentist characteristics: a practical solution, Biometrics