Program in Regulatory Science Clinical Trial Designs
The work of the Program in Regulatory Science focuses on the development, application, theoretical study, and software for innovative clinical trial designs. Areas of our research include:
Platform Designs
We study platform designs, which allow investigators to add new and remove existing experimental arms on a clinical study, either when new experimental drugs become available, or when sufficient information on the efficacy of an experimental treatment has been gathered. Although controlled multi-arm trials are more efficient than two-arm studies, because the control arm is not replicated to evaluate multiple treatments, they are rarely utilized. A drawback is the requirement that all therapies, often drugs from different companies, must be available for testing at the onset of the trial. Platform trials, by contrast, remedy this constraint and can substantially improve the efficiency of screening studies that evaluate new treatments in their early stages of development.
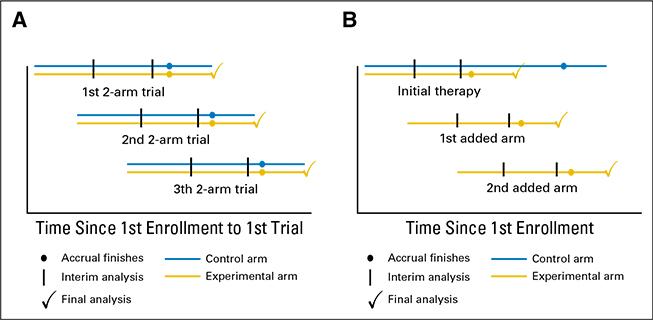
Read more: Ventz et al 2017, Designing Clinical Trials That Accept New Arms: An Example in Metastatic Breast Cancer, Journal of Clinical Oncology
Definition of Adaptive Randomization Probabilities
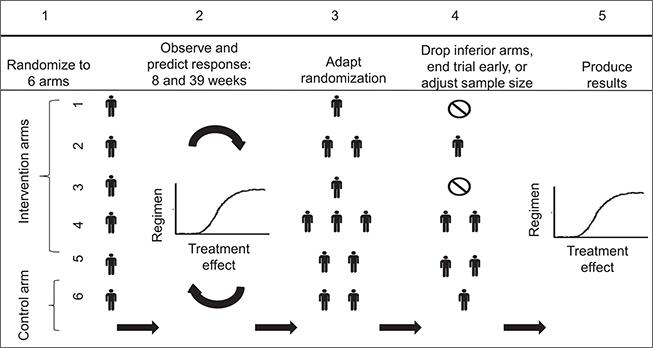
We propose new Bayesian response-adaptive randomization rules. Most response-adaptive randomization schemes have been designed to increase the number of patients that receive an effective treatment during the clinical trial. We developed approaches to translate early evidence and available information on treatments into suitable randomization probabilities during the course of the study. In multi-arm studies, we define Bayesian randomization probabilities that, at completion of the study, minimize uncertainty of the treatment effects of multiple experimental arms as quantified by standard statistical metrics.
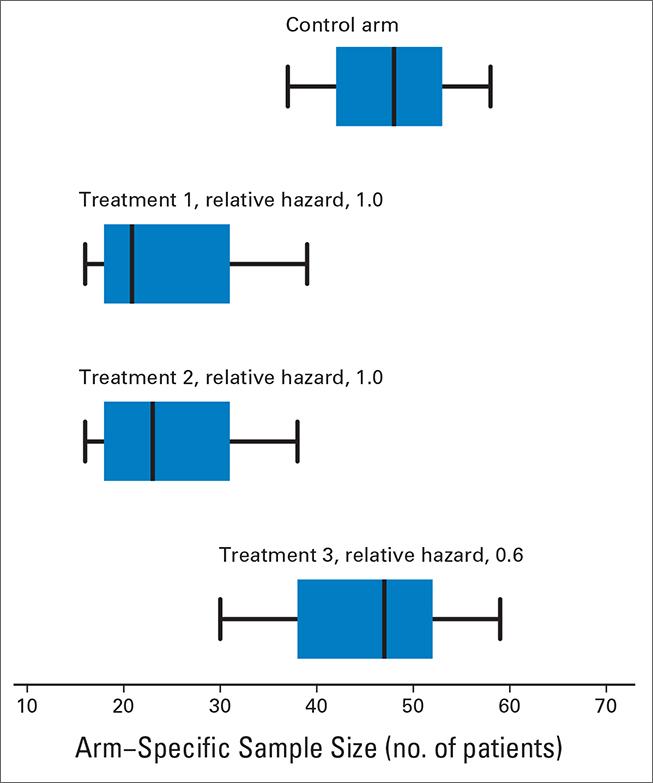
Read more: Trippa et al 2012, Bayesian adaptive randomized trial design for patients with recurrent glioblastoma, Journal of Clinical Oncology
Biomarker-Driven Clinical Trials
Biomarkers define patient subgroups, which are fundamental in clinical studies where investigators expect different treatment effects across biomarker profiles; the primary goal is to identify the subpopulation for which the experimental therapy shows evidence of treatment efficacy and to exclude other subpopulations for which it does not. To facilitate this, Bayesian response-adaptive designs map accumulating information on experimental treatments into randomization probabilities that vary across patient subgroups. We recently studied the use of Bayesian adaptive randomization in basket clinical trials, which enroll multiple cancer types. We modeled the treatment effects by allowing variations both across cancer types and across biomarker subgroups.
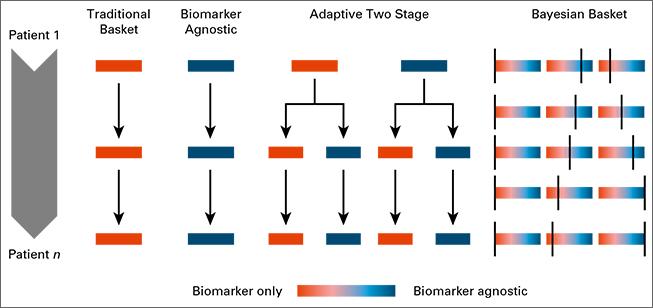
Read more: Trippa Alexander 2016, Bayesian Baskets: A Novel Design for Biomarker-Based Clinical Trials, Journal of Clinical Oncology
Joint Modeling of Multiple Endpoints
Our collaborations motivated work on joint Bayesian modeling of surrogate and primary endpoints. The goal of this work is to produce randomization probabilities that mirror, during the course of the clinical trial, both early efficacy results for surrogate endpoints and preliminary evidence of treatment effects for primary endpoints. In cancer trials, we use the duration of progression-free status to predict patient survival using Bayesian methods. Joint modeling of multiple endpoints allows us to use adaptive randomization in clinical settings where the primary outcome becomes available months or years after treatment assignment.
Read more: Trippa et al 2015, Combining progression-free survival and overall survival as a novel composite endpoint for glioblastoma trials, Neuro Oncology
False Positive Results, P-values and Bayesian Studies
We propose and study methods that allow frequentist analyses, including rigorous p-values and confidence intervals, at completion of Bayesian clinical trials. Clinicians, scientific review panels, and other stakeholders in the clinical trials arena are familiar with key statistical concepts from the frequentist literature: type I error rates, hypothesis testing and confidence intervals to name a few. Methodologies that combine Bayesian designs and frequentist analyses can accelerate the adoption of innovative adaptive designs, and simplify their acceptance from stakeholders involved in clinical studies.
Read more: Ventz et al 2015, Bayesian designs and the control of frequentist characteristics: a practical solution, Biometrics